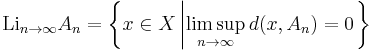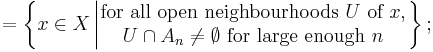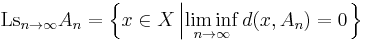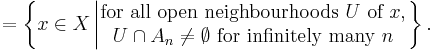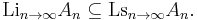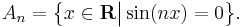Kuratowski convergence

In mathematics, Kuratowski convergence is a notion of convergence for sequences (or, more generally, nets) of compact subsets of metric spaces, named after the Polish mathematician Kazimierz Kuratowski. Intuitively, the Kuratowski limit of a sequence of sets is where the sets "accumulate".

1 Definitions
2 Properties
3 Examples
4 References

Definitions

Let (X, d) be a metric space. For any point x ∈ X and any non-empty compact subset A ⊆ X, let

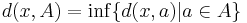$d(x, A) = \inf \{ d(x, a) | a \in A \}$ .

For any sequence of such subsets A_n ⊆ X, n ∈ N, the Kuratowski limit inferior (or lower closed limit) of A_n as n → ∞ is

$\mathop{\mathrm{Li}}_{n \to \infty} A_{n} = \left\{ x \in X \left| \limsup_{n \to \infty} d(x, A_{n}) = 0 \right. \right\}$

$= \left\{ x \in X \left| \begin{matrix} \mbox{for all open neighbourhoods } U \mbox{ of } x, \\ U \cap A_{n} \neq \emptyset \mbox{ for large enough } n \end{matrix} \right. \right\};$

the Kuratowski limit superior (or upper closed limit) of A_n as n → ∞ is

$\mathop{\mathrm{Ls}}_{n \to \infty} A_{n} = \left\{ x \in X \left| \liminf_{n \to \infty} d(x, A_{n}) = 0 \right. \right\}$

$= \left\{ x \in X \left| \begin{matrix} \mbox{for all open neighbourhoods } U \mbox{ of } x, \\ U \cap A_{n} \neq \emptyset \mbox{ for infinitely many } n \end{matrix} \right. \right\}.$

If the Kuratowski limits inferior and superior agree (i.e. are the same subset of X), then their common value is called the Kuratowski limit of the sets A_n as n → ∞ and denoted Lt_n→∞A_n.

The definitions for a general net of compact subsets of X go through mutatis mutandis.

Properties

Although it may seem counter-intuitive that the Kuratowski limit inferior involves the limit superior of the distances, and vice versa, the nomenclature becomes more obvious when one sees that, for any sequence of sets,

$\mathop{\mathrm{Li}}_{n \to \infty} A_{n} \subseteq \mathop{\mathrm{Ls}}_{n \to \infty} A_{n}.$

I.e. the limit inferior is the smaller set and the limit superior the larger one.

The terms upper and lower closed limit stem from the fact that Li_n→∞A_n and Ls_n→∞A_n are always closed sets in the metric topology on (X, d).

Examples

Let A_n be the zero set of sin(nx) as a function of x from R to itself

$A_{n} = \big\{ x \in \mathbf{R} \big| \sin (n x) = 0 \big\}.$

Then A_n converges in the Kuratowski sense to the whole real line R.

References

Kuratowski, Kazimierz (1966). Topology. Volumes I and II. New edition, revised and augmented. Translated from the French by J. Jaworowski. New York: Academic Press. pp. xx+560. MR 0217751

Kuratowski convergence

Contents

Definitions

Properties

Examples

References